Jesus M. Cortes, Paolo Bonifazi, Iñaki Escudero, Beatriz Mateos, Miguel Angel Muñoz, Sebastiano Stramaglia, Jesus M. Cortes, Borja Camino-Pontes, Antonio Jimenez-Marin, Javier Rasero, Asier Erramuzpe, Stephan Swinnen, Iñigo Gabilondo, Matthieu P. Boisgontier, Lisa Pauwels, Laiene Olabarrieta-Landa, Manuel Fernandez Martinez, Juan Carlos Arango Lasprilla, David Drijkoningen, Daniele Marinazzo, Jolien Gooijers, Ibai Diez. Brain Hierarchical Atlas: Multi-Scale versus Optimal Strategies in the Pathological Brain. OHBM 2019 – Organization for Human Brain Mapping [pdf]
Introduction:
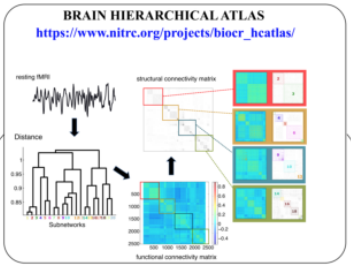
Elucidating the intricate relationship between brain structure and function is a key challenge for modern neuroscience. Recent progress in neuroimaging has helped advance our understanding of this important issue, with diffusion images providing information about structural connectivity (SC) and functional magnetic resonance imaging shedding light on resting state functional connectivity (FC). Here, we adopt a systems approach that uses modular hierarchical clustering to combine SC and FC datasets into a common atlas that we name the brain hierarchical atlas (BHA) (Diez et al. 2015). Here, we extend this work by focusing on two strategies that can be applied when using BHA: a multiscale approach vs an optimal brain partition. For the multiscale approach we show rst how brain networks reorganize after traumatic brain injury in a pediatric population (Diez et al 2017). Second, how structure-function brain networks can accurately predict brain aging (Bonifazi et al 2018). From the alternative strategy of the optimal brain partition, we show rst a complete characterization of the progressive alterations in structural connectivity patterns across severity stages in Alzheimer’s disease (Rasero et al 2017) and second, that the default mode network has a redundant role along lifespan (Camino-Pontes et al. 2018).
Methods:
Structural connectivity (SC) matrices were obtained by counting the number of bers connecting each individual pair of ROIs. Functional connectivity (FC) matrices were calculated by obtaining the Pearson correlation coef cient between the rs-fMRI time series for each ROI pair. A hierarchical agglomerative clustering (HAC) was applied to extract brain modules on different scales. The rst step was to select a set of features to describe each ROI that FC was used the connectivity matrix of a given ROI to the other ones (here, 2514 values for each ROI). Next, we applied the cosine distance to perform the clustering. For SC, the feature vector was based on the distance, de ned as one minus the ber number normalized between 0 and 1. For each module of a given partition, the similarity between the corresponding modules of SC and FC was calculated using the Sorensen index (and similar results were obtained with Jaccard similarity). Newman modularity (Q) between FC and SC was used to address modularity for a given brain partition. Finally, the optimal brain partition was obtained based on the cross- modularity (X) between SC and FC, de ned as the geometric mean between the modularity of SC, the modularity of FC, and the mean Sorensen similarity between structural and functional modules. The value of M=20 was the one maximizing X, which provides the optimal brain partition. Alternatively, an arbitrary number of M provides the multi-scale approach, as this allows to go from M=1 (entire brain) to M the number of ROIs (here, 2514).
Results:
Multiscale approach 1: Network enhancement after traumatic brain injury (N=14). Multiscale approach 2: Brain networks prediction of aging (N=155).
Optimal brain partition 1: Progressive alterations of diffusion tensor connectivity across severity stages in Alzheimer’s Disease (N=144).
Optimal brain partition 2: Redundant role of the DMN along lifespan (N=164).
Conclusions:
The use of the BHA guarantees four conditions simultaneously: (1) that the dynamics of voxels belonging to the same module is very similar, (2) that those voxels belonging to the same module are structurally wired by white matter streamlines, (3) when varying the level of the hierarchical tree, it provides a multi-scale brain partition, where the highest dendrogram level occurs for M = 1 (coincident with the entire brain), whereas the lowest level M = 2514 correspond as many modules as ROIs, (4) the atlas with M = 20 modules is optimal based on crossmodularity.