J.M. Cortes, J. Goñi, M.A. Muñoz and D.R. Chialvo. Generic dynamics at criticality links brain structure to function. Frontiers in Neuroinformatics, 2013 [pdf]
The relation, influence, and constraints between structure and function of the human brain is not yet well understood, even for the widely studied resting state. In the last decade, different topological descriptors, and dynamical models such as neural mass or more complicated coupling models have shown how dynamics produced upon a given structure can partially map the empirical functional connectivity. In this context, a number of experimental findings seem to support the conjecture that the brain works at (or near) criticality (for review see [1] and references therein). Theoretical approaches have shown that systems operating at this critical regime show multiple functional advantages, such as maximal memory storage, information transfer and dynamic range. Universality –stating that model specific details should not matter at criticality– is inherent to critical phenomena. Instead, only a few key traits such as dimensions, symmetries and conservation laws are relevant. Based on these ideas, we show here how very simple dynamical models running upon a given structural connectivity and tuned to its critical point can reproduce some relevant features of brain functioning at its resting state. It will also be shown how modifying some key aspects of the underlying structural connectivity affects the mapping between criticality and the empirical functioning.
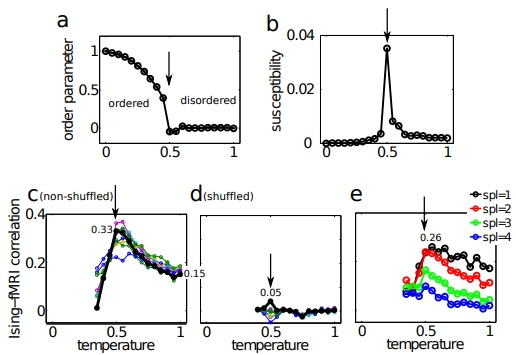
In order to implement a parsimonious dynamics, we have followed previous studies [2] and considered the Ising model in which the network nodes have been linked by pairwise interactions and performed Monte Carlo simulations using the Metropolis rule, which drives the system to its corresponding equilibrium state at any given temperature [3]. For experimental structural and functional pairwise interactions, matrices representing a human connectome and its functional connectivity [4] were used. They consist of a partition of the human brain cortical surface in 998 regions, each of one resembling approximately 150 mm2.
Simulations of the Ising model performed on the top of the structural connectivity matrix permitted to produce dynamics and subsequent in-silico functional connectivity matrices at different temperature values. Those matrices were then compared with the empirical functional connectivity. Interestingly, the similarity between empirical and in-silico matrices reach a maximum nearby the criticality temperature range. Based on these findings, we further analyse different aspects of the dynamics of the Ising dynamics and its connection to the rs-fMRI dynamics by using different Information-theory approaches that has been previously obtained for the Ising model.
References:
[1] D. R. Chialvo. Emergent complex neural dynamics. Nature Phys, 6:744–750, 2010.
[2] D. Fraiman, P. Balenzuela, J. Jennifer, and D. R. Chialvo. Ising-like dynamics in large-scale functional brain networks. Phys Rev E, 79:061922, 2009.
[3] J.J. Binney, N.J. Dowrick A.J. Fisher, and M.E.J. Newman. The Theory of Critical Phenomena. Oxford University Press, Oxford, 1993.
[4] P. Hagmann, L. Cammoun, X. Gigandet, R. Meuli, C.J. Honey, V.J. Wedeen, and O. Sporns. Mapping the Structural Core of Human Cerebral Cortex. PLoS Biol, 6:e159, 2008.