J. Marro, J.J. Torres and J.M. Cortes. Complex behavior in a network with time-dependent connections and silent nodes. Journal of Statistical Mechanics P02017, 2008 [pdf]
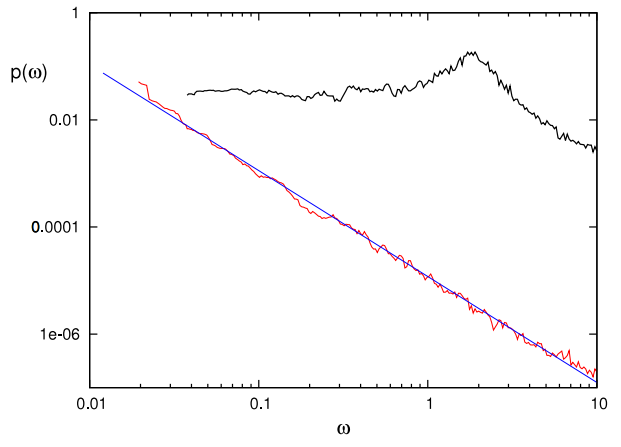
We studied, both analytically and numerically, excitable networks in which connections are time-dependent and some of the nodes remain silent at each time step, and we show that these two features may induce intriguing functional complexity. More specifically, we consider (a) a heterogeneous distribution of connection weights such that, depending on the current degree of order, some connections are reinforced/weakened with strength (a) on short timescales, and (b) that only a fraction of nodes are simultaneously active. The resulting dynamics has attractors which, for a range of values and exceeding a threshold, become unstable, the instability depending critically on the value of the number of nodes being active. We observe that (i) the activity describes a trajectory in which the close neighborhood of some of the attractors is constantly visited, (ii) the number of attractors visited increases with the number of nodes being active and (iii) the trajectory may change from regular to chaotic and vice versa as this parameter is, even slightly modified. Furthermore, (iv) time series show a power-law spectra under conditions in which the attractors’ space tends to be most efficiently explored. We argue on the possible qualitative relevance of this phenomenology to networks in several natural contexts.