S. Stramaglia, J.M. Cortes, L. Angelini, M. Pellicoro and D. Marinazzo. Information flow in Ising models on brain networks. V.M. Mladenov and P.C. Ivanov (Eds.): NDES 2014, CCIS 438, pp. 301–308, 2014 [pdf].
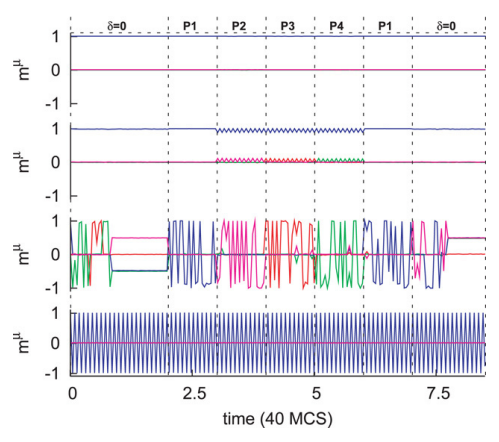
We analyze the information flow in the Ising model on two real networks, describing the brain at the mesoscale, with Glauber dynamics. We find that the critical state is characterized by the maximal amount of information flow in the system, and that this does not happen when the Ising model is implemented on the two-dimensional regular grid. At criticality the system shows signatures of the law of diminishing marginal returns, some nodes showing disparity between incoming and outgoing information. We also implement the Ising model with conserved dynamics and show that there are regions of the systems exhibiting anticorrelation, in spite of the fact that all couplings are positive; this phenomenon may be connected with some evidences in real brains (the default mode network is characterized by anticorrelated components).